It’s a Bluesky link but he use adult tags as de facto “spoiler” tags. The problem is that content is hidden if you’re not logged into Bluesky. Here’s a Bluesky mirror site to show the entire thread…
https://subium.com/profile/c0nc0rdance.bsky.social/post/3kpkcq2ecws22
A huge hint…
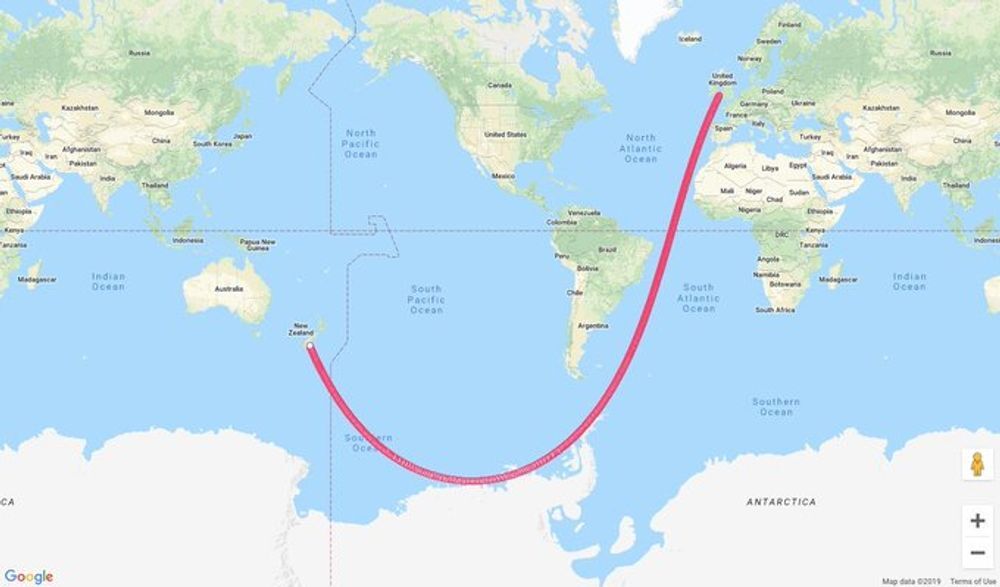

No we dont live in a 3d space. That’s a mathematical model used to model reality so as to be able to ignore details deemed unecessary for whatever the model is for. It’s a tool to approximate reality not reality itself.
And for the purposes of traversing our globe a 3rd dimension is unecessary so why include that in your model?
And even if, its blatantly obvious that the OOP is asking for a straight line in a 2d perspective, not on a map, but on the globe itself because any projection of a globe into a flat space will take the straightness out of a straight line.
How would you begin to describe points in the spaces we are discussing? I feel this is a fair question, because in an earlier reply you suggest to picking a point and walking there.
For the surface of a sphere, the most natural way many people would choose to do this would be using the tuples (x,y,z) in R3 and restricting this space to a subspace by the equation X2 + Y2 + Z2 = r2, were r is the radius of the sphere. Give a model which can describe points and lines on the surface of a sphere with less than 3 dimensions; i.e., define a space for the surface of a sphere with fewer than 3 dimensions.
The problems with trying to do this by defining a conformal map from 2 dimensional projective spaces to 3 dimensional surfaces is the reason whole books are written about projective geometry.
This doesn’t make sense. Which projection? The natural one? Such a map is guaranteed to not be a bijection and is potentially not well-defined. Without a clear way of doing this map, you can’t say anything about what happens to lines under the image of such a map.
I agree with this at least, I too am tired of the mathematical platonism dominating the public discourse.
latitude and longitude
just put the poles wherever it’s convenient
idk, to me this is kinda semantics, whether or not we say a 2d surface in 3d space is 2d or 3d.
just assume “straight line” refers to a geodesic on the surface, then you can use whatever coordinates you want.
TL;DR being able to talk about curvature in a mathematical way outside of a euclidean space is a chore because it needs differentiation and its best to let your intuition guide you when talking about these concepts because “walking straight on a sphere” is imo clear enough.
A differentiable manifold holds the key. Start with a topological space. So the points in ℝ3 you described along with the by the ℝ3 induced topology is indeed the goto. Note that the radius of the sphere no longer matters as any sphere can be projected onto any other homeomorphically.
Then define homeomorphic maps from open subsets of the ℝ2 onto the sphere until its covered. At least two such maps are necessary. The key is now that the maps necessarily have to overlap on the sphere and we thus get maps from an open subset in the ℝ2 to another open subset of the ℝ2 by using one map go to the sphere and the inverse of another overlapping map to go back to the ℝ2. By requiring that these functions be diffeomorphic we transport the structure required for calculus to the sphere and we can talk about the curvature of a path. Then we can observe the existance of straight line by describing a path with no curvature on the sphere.
Because of the requirement of diffeomorphism the structure is unique, i. e. any other such structure can be diffeomorphically mapped to eachother and we can switch out maps as we please without changing any properties of the objects constructed.
By this I meant that if you take any projection of the sphere onto a flat surface, use it to project a line without curvature on the sphere to the flat surface the line thusly obtained will be curved w.r.t. the structure of the flat surface.
edit: this is obviously incorrect as any world map will show apologies. I should have said that there is a projection for any straight line on the sphere which will map it to a curved one in the 2d space.