No, I’m not putting this in /c/electoralism , for reasons found in the third paragraph
Most people know there’s first-past-the-post and there’s ranked-choice. But I’ve recently learned there’s a much longer list than that, and they all have pros and cons.
Somecomrades would say 🙄yeah bourgeois elections who cares🙄 but that is wrong: the mathematics applies to all voting. It’s the engineering side of the question: “If we have a bunch of people, maybe a hundred, maybe a million, how do we decide what the collective will is in the fairest way?” The name of the field is social choice theory because a social group is trying to make a choice.
You: oh bourgeois elections are a farce lol
Me: exactly and that’s why we need to study how can voting be not a farce
First-past-the-post gets a hard time, and deservedly so. But the people who say “first-past-the-post bad, ranked choice good” are oversimplifying. It turns out there are all these mathematical trade-offs, and it is formally provable that there is no perfect system.
Most ranked choice voting systems* can suffer from a crazy effect where getting more votes makes you lose. The technical name for this is a monotonicity failure because mathematicians are shit with names. (*There are theoretical ranked-choice votings that don’t fail monotonicity, but I don’t know of any being applied in a political system. Companies probably have used them.)
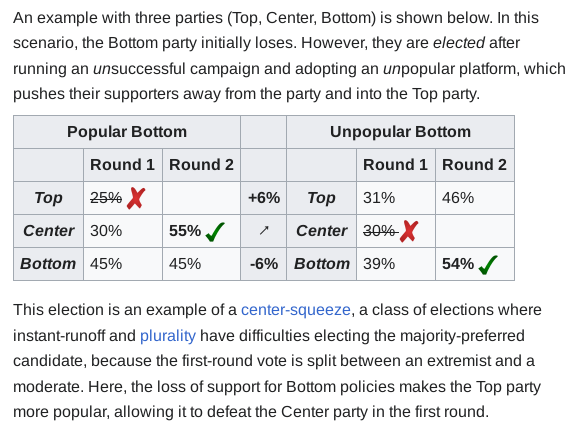
In the ‘Popular Bottom’ Scenario,  gets 45% of the vote and isn’t elected; but in the other scenario he gets 39% and is elected. What happened is he lost supporters to a rival (Top) who eliminated his other rival (Center) for him, so he was able to sneak in.
gets 45% of the vote and isn’t elected; but in the other scenario he gets 39% and is elected. What happened is he lost supporters to a rival (Top) who eliminated his other rival (Center) for him, so he was able to sneak in.
First-past-the-post doesn’t have this problem: more votes is always better. But it has plenty of other problems. The USA system fails the no favorite betrayal criterion catastrophically; that’s the criterion that you should be able to vote for who you like best. Usans “have to” vote for a candidate they hate.
This page summarises it pretty well: https://en.wikipedia.org/wiki/Comparison_of_voting_rules with tables comparing the different traps multi-winner systems fall into and the traps single-winner systems fall into.
Some cool systems:
-
PDF – “This paper discusses the protocol used for electing the Doge of Venice between 1268 and the end of the Republic in 1797”
Anyway, interesting stuff to think about if we design democratic/anarchistic systems for collective decision-making. It wouldn’t have to be electing representatives, it could be voting on policies, same maths either way.


The maths you’re talking about rank fairness by how many (percentage) of the voters end up with a satisfactory outcome. There’s a saying that the only perfectly fair voting system is a dictatorship, because only one person gets to vote, and they always get what they want. All other systems have flaws. As in most things, you are trying to maximize fairness.
The secondmost fair system is the Condorcet method, and in fact other systems are usually ranked by how often the winner is the Condorcet winner. The reason nobody uses Condorcet itself is that it’s extremely complicated, and one tradeoff in any election system is whether the voters are able to understand, and therefore trust, the system. The more simple the system, the easier to explain, and the more people trust the outcome. FPTP’s singular virtue is that it’s stupid simple, and any idiot can understand it. Condorcet is at the other extreme, and other systems fall in between.
Ranked Choice is reasonably simple, and produces more Condorcet winners than FPTP. STAR is a little more complicated, but also a little more fair. And, yes, every system has edge cases where the wrong person - someone other than the Condorcet winner - is elected.
The objective is to get there best outcome for the most people, which includes strategies like reducing motivations for strategic voting, and allowing for compromise. The benefit to nearly every system other than FPTP is that they allow for the election of maybe nobody’s favorite, but someone that it’s acceptable to 100% of the voters; this is considered “more fair” than 51% getting their favorite, and 49% get someone they actively object to.
As you’ve found, no system is perfect (except dictatorship), and you can always concoct edge cases where the method fails; but that doesn’t mean that some aren’t better or worse than others, fairness-wise.
One absolute truth, though, is that FPTP is the provably worst system in terms of producing fair outcomes. In the US, Ranked Choice is slowly replacing FPTP in local elections. It’s not the best, but it’s better, and it’s understandable, could be verified by hand, and doesn’t require a computer to produce results within a reasonable time. In this case, Perfect is the enemy of Good, and while we could debate endlessly on the merits of various systems, replacing FPTP with Ranked Choice is a definite improvement.
It’s very demonstrably not even the case in most cases we deal with that everyone getting something acceptable is more fair than some getting their favorite. Maybe in a hyper-egalitarian situation that is the case, but in most cases there are some who have more at stake and are more vulnerable. It’s important to remember what it means for a situation to be fair, a situation that we would impartially approve of (say, by not knowing who we are in a situation and acting in our self-interest). In such a situation, you’d want those with the most at stake to get their way, even if they’re the 49% and the rest aren’t happy with it. If we don’t accept that then it’s really unclear why we anarchists give a shit about consensus.
In this case, everyone may find a particular choice acceptable, but find the overall decision-making situation unacceptable. Like, if you’re disabled, and you rarely get to eat foods that you enjoy, and your friends invite you out, you may find certain restaurants acceptable because they at least have fries or a salad you can eat without throwing up but you’d love to go to one of two restaurants. Your friends eat out every other week and can eat pretty much anything, minestrone, rotini, a whole plant-based ice cream cake each, whatever. You may find those acceptable restaurants acceptable, but find it unacceptable that your needs and desires don’t outweigh the others for this decision-making.
It’s not fair. It’s obviously not fair, even though everyone is getting the acceptable option. In this case, going where you want, even if the others would prefer not to go to those restaurants, is fair. And most group decision-making situations today are like this.