- cross-posted to:
- nonpolitical_memes@lemmy.ml
- cross-posted to:
- nonpolitical_memes@lemmy.ml
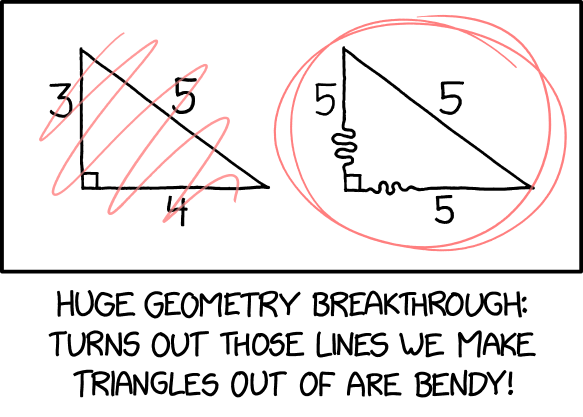
When you miss one important constraint in your CAD project.
Oh man I felt this.
Wouldn’t the angles need to be interior?
They are all interior to the meme

This meme seems to be in a 16:9 ratio making it a rectangle.
also the sides must be straight
It’s 2024 now… Not everyone has to be straight anymore!
If you want to claim you are a square, you need.
WOW! just wow, do you hear yourself?
It’s actually illegal
Believe it or not, straight to jail.
Hi.
Polar coordinate straight
Define straight in a precise, mathematical way.
The tangent of all points along the line equal that line
Only true in Cartesian coordinates.
A straight line in polar coordinates with the same tangent would be a circle.
EDIT: it is still a “straight” line. But then the result of a square on a surface is not the same shape any more.
A straight line in polar coordinates with the same tangent would be a circle.
I’m not sure that’s true. In non-euclidean geometry it might be, but aren’t polar coordinates just an alternative way of expressing cartesian?
Looking at a libre textbook, it seems to be showing that a tangent line in polar coordinates is still a straight line, not a circle.
I’m saying that the tangent of a straight line in Cartesian coordinates, projected into polar, does not have constant tangent. A line with a constant tangent in polar, would look like a circle in Cartesian.
Polar Functions and dydx
We are interested in the lines tangent a given graph, regardless of whether that graph is produced by rectangular, parametric, or polar equations. In each of these contexts, the slope of the tangent line is dydx. Given r=f(θ), we are generally not concerned with r′=f′(θ); that describes how fast r changes with respect to θ. Instead, we will use x=f(θ)cosθ, y=f(θ)sinθ to compute dydx.
From the link above. I really don’t understand why you seem to think a tangent line in polar coordinates would be a circle.
geodesic
I knew math was homophobic!
This is merely a projection of a square on the surface of a cone projected onto a plane.
This is also not a polygon. It has infinite and 2 sides at the same time.
This actually has six right angles if you include exterior ones.
Kinda forgot the sides being parallel part. Like missing a step in assembling IKEA furniture, its not gonna turn out right.
You don’t normally need to specify that the sides are parallel if you specify four right angles.
Also pretty sure definition of a shape requires only one enclosed or contiguous area.
This one is enclosed and contiguous though, the lines of the triangle end where the circular line starts. (The rest is just a drafting residue.)
No, it is 2 contiguous regions. The line of separation is the bounding line of a “shape.”
Otherwise, the entire whitespace outside of the region is also part of the shape, as is anything it touches.
OK, imagine the space outside of the shape is black, or see through or whatever.
Well then the line of separation means nothing and then you’ve lost two right angles to the contiguous void.
Why? Does a cube floating in the void not have angles?
Without a distinction of where the cube begins or ends it does not because there is no cube and there are no angles.
The angle of the triangle that protrudes into the circular part is not a right angle.
My apologies you’re correct, you lose two right angles.
Those arc sides are parallel in polar coordinates.
Anarchy geometry
If anyone makes this community, let me know please.
i will make it, but i won’t tell you
NOOOOOoooo…!
deleted by creator
Easy there Diogenes.

Out of 4 lines
A square has all right angles inside the structure. This thing has two inside and two outside.
If you add that to the definition, you could still have a “square” with a segment of a circle connecting the edges in the middle
Then that section would be of a shorter length.
Ah, got me
But arent the ones from the circle 90 degrees on the inside of the circle as well? The squares could’ve just as well been placed on the other side of the (circle) lines.
No, the two angles are not equal. Outside/inside angles add up to two π radians. A square has four interior angles of 1/2 π radians, and four exterior angles of 3/2 π radians.
This is true, however now it has 4 inside and two outside the structure, so it now has something a square doesn’t has.
Parallelogram.
This has an infinite number of sides
This is what AI would give you after countless tries strating with a triangle and having gone up the Pentagon and down to two pairs of unconnected parallel lines…but what if all equally sized lines were connected? Bam! This
Fun Fact: It is very difficult to get any of the image generators to make a pentagon.
I thought this couldn’t be true, so using one of the newer models (4bit flux) I told it to make a 5 sided star, and then put lines around the outside
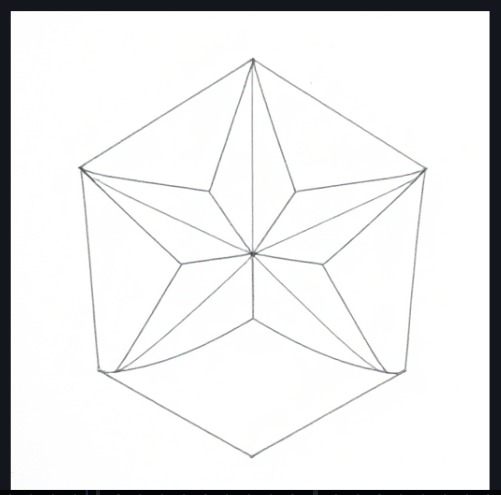
lol this is very weird, did they forbid it from looking at pentagons in the training data or something? it can’t do The Pentagon either, it gives it 8-12 sides instead
I don’t really know, but I think it’s mostly to do with pentagons being under-represented in the world in general. That and the specific way that a pentagon breaks symmetry. But it’s not completely impossible to get em to make one. After a lot of futzing around, o1 wrote this prompt, which seems to work 50% of the time with FLUX [pro]:
An illustration of a regular pentagon shape: a flat, two-dimensional geometric figure with five equal straight sides and five equal angles, drawn with black lines on a white background, centered in the image.

quick test, with that prompt and flux schnell gguf 4 bit again:
- pentagon: 1
- hexagon: 9
- heptagon: 2
- octagon: 7
- decagon: 1
it seems a lot stupider than pro lol
Poor Pac-Man does not look quite okay… :-(
That’s a Pac-lapse.
A square? A square?! Wake up sheeple! That things not even a rombus! Don’t you see the lies? Look at the lines! Look! Not all rhombuses are squares, but all squares are rhombuses! All squares are rhombuses and look at this thing they try to call a square. Where are the parallel lines? There’s got to be parallel lines, don’t you see, or then it’s not a rombus and all squares are rhombuses. Don’t forget that, don’t let them take that fact from you and perpetuate their geometric lies. Does no one even remember what a rombus is? This is, this is basic geometry here that you should have learned in middle school or elementary school, but then you just forget it, and let people trick you with these misleading definitions and fancy diagrams but you have to remember that a Square. Is. A. Rombus.
And all rhombus are parallelograms. By definition opposing sides must be parallel.
YES. YES! A square is a rombus is a parallelogram! You see it too! There are no parallels in this diagram, only lies and trickery!
This is why proper geometry is always well defined.
You have shown me the truth
thinking outside the square
270°≠90°
You could say a regular square has 4 270° exterior angles
Now make a square out of squiggly yarn
String theorists claim this is the true shape of spacetime!